Прямокутний трикутник – повний гід для школярів

Що таке прямокутний трикутник?

Прямокутний трикутник — це трикутник, у якого один з кутів дорівнює 90 градусів. Такий кут називається прямим. Решта два кути завжди гострі, тобто менші за 90 градусів. Усього сума всіх кутів у будь-якому трикутнику дорівнює 180 градусів.

Основні елементи прямокутного трикутника

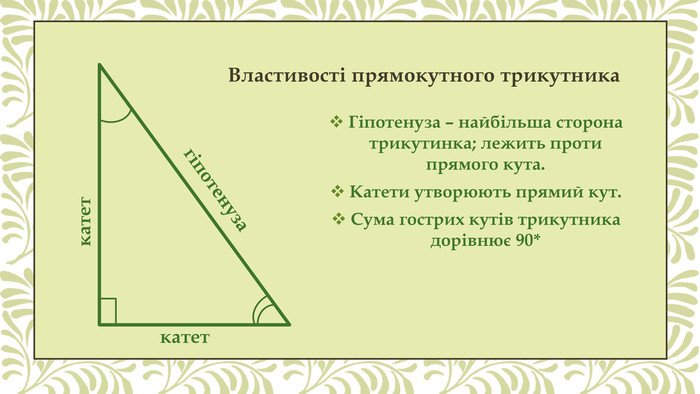
У кожному прямокутному трикутнику можна виділити три важливі частини:

• Гіпотенуза — це найдовша сторона, що лежить навпроти прямого кута.
  
• Катети — це дві інші сторони, які утворюють прямий кут.
  

Коли ми знаємо ці елементи, легко виконувати різні обчислення.

Чому прямокутний трикутник важливий?

По-перше, він є основою багатьох математичних задач. По-друге, за його допомогою легко вивчати поняття синуса, косинуса і тангенса. Нарешті, знання про прямокутний трикутник допоможе розв’язувати реальні задачі — наприклад, як підрахувати висоту дерева або нахил сходів.

Теорема Піфагора

Одне з найвідоміших правил, що пов’язане з прямокутним трикутником, — це теорема Піфагора. Вона звучить так:

Квадрат гіпотенузи дорівнює сумі квадратів катетів.

У вигляді формули це виглядає так:

r

CopyEdit

c² = a² + b²

де c — гіпотенуза, a і b — катети.

Приклад задачі з прямокутним трикутником

Уявімо, що один катет дорівнює 3 см, а інший — 4 см. Щоб знайти гіпотенузу, підставимо значення у формулу Піфагора:

r

CopyEdit

c² = 3² + 4² = 9 + 16 = 25

Отже,

ini

CopyEdit

c = √25 = 5 см

Властивості прямокутного трикутника

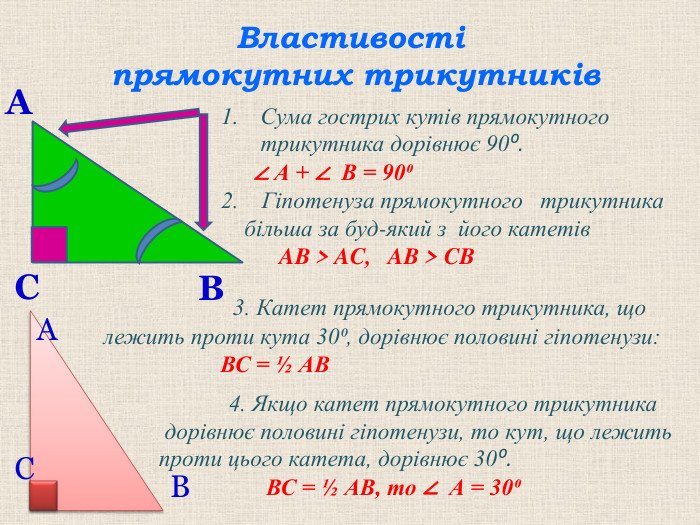
Ось кілька ключових властивостей, які варто запам’ятати:

• Один з кутів завжди прямий.
  
• Сума інших двох кутів дорівнює 90 градусів.
  
• Гіпотенуза завжди довша за будь-який катет.
  
• Висота, опущена з вершини прямого кута на гіпотенузу, утворює два менших прямокутних трикутника.
  

Прямокутний трикутник у координатній площині

Ще одне важливе застосування — у координатній геометрії. Якщо координати трьох точок утворюють прямокутний трикутник, це легко довести за допомогою теореми Піфагора. Достатньо знайти довжини трьох сторін і перевірити співвідношення.

Тригонометричні функції в прямокутному трикутнику

Тригонометрія тісно пов’язана з прямокутними трикутниками. Для гострого кута α використовують наступні співвідношення:

• Синус (sin): відношення протилежного катета до гіпотенузи.
  
• Косинус (cos): відношення прилеглого катета до гіпотенузи.
  
• Тангенс (tan): відношення протилежного катета до прилеглого.
  

Ці функції важливі для обчислення сторін і кутів.

Як побудувати прямокутний трикутник?

Щоб побудувати прямокутний трикутник, виконай такі кроки:

1. Намалюй пряму лінію — це буде один катет.
   
2. З кінця цієї лінії побудуй перпендикуляр — це другий катет.
   
3. З’єднай кінці катетів — це буде гіпотенуза.
   

Тепер у тебе є справжній прямокутний трикутник!

Де зустрічаються прямокутні трикутники у житті?

Прямокутні трикутники можна знайти всюди:

• У сходах і пандусах.
  
• У будівлях та мостах.
  
• У кресленнях і картах.
  
• Навіть у спорті — наприклад, під час стрибків у висоту.
  

Тому розуміння їх структури корисне в різних галузях.

Геометричні задачі з прямокутним трикутником

Часто в задачах треба знайти невідому сторону або кут. Для цього використовують:

• Теорему Піфагора.
  
• Тригонометричні функції.
  
• Подібність трикутників.
  

Порада: завжди починай з малюнка. Це допоможе краще зрозуміти умову задачі.

Подібність прямокутних трикутників

Прямокутні трикутники вважаються подібними, якщо:

• У них рівні кути.
  
• Сторони пропорційні.
  

Ця властивість дозволяє вирішувати складніші задачі, навіть коли відомо мало даних.

Прямокутний трикутникк і вписане коло

У кожен прямокутний трикутникк можна вписати коло. Центр такого кола лежить на бісектрисі прямого кута. Радіус цього кола легко обчислюється, якщо відомі всі сторони трикутника.

Часті помилки у роботі з прямокутними трикутниками

Щоб уникнути непорозумінь, пам’ятай наступне:

• Не плутай катети і гіпотенузу.
  
• Перевіряй, чи точно один з кутів дорівнює 90°.
  
• У задачах з координатами уважно використовуй формули відстаней.
  

Ці поради допоможуть уникнути зайвих проблем.

Повторення: найголовніше про прямокутний трикутникк

• Має один прямий кут.
  
• Складається з гіпотенузи і двох катетів.
  
• Теорема Піфагора — головне правило.
  
• Часто використовується у геометрії, фізиці та повсякденному житті.
  

Читати далі: Таблиця косинусів – Повний гід для школярів і студентів

Часті запитання: Прямокутний трикутник